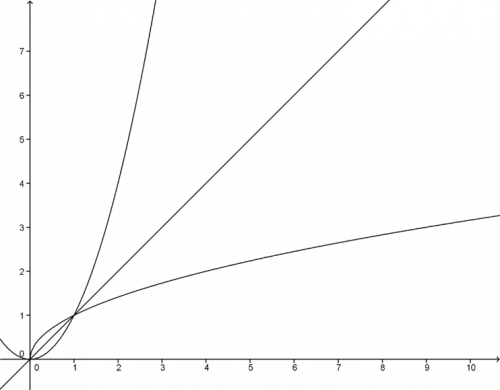
Funkce \(y=\sqrt x\) je inverzní k \(y=x^2\) na intervalu \(x\in (0;\infty)\). Co je to inverzní funkce? Nyní nám postačí informace, že funkce jsou k sobě navzájem inverzní, právě když jsou souměrné podle osy prvního a třetího kvadrantu. Osvětlíme obrázkem.
Osa prvního a třetího kvadrantu je lineární funkce definovaná předpisem \(y=x\).
Příklad 9
\(y=\sqrt{x-4}+2\)
Postup při načrtání je analogický jako u předchozích příkladů. Nejdříve se podíváme na proměnnou \(x\) a jejího parťáka v závorce. Hledáme nulový bod odmocniny, abychom zjistili, o kolik jednotek po ose \(x\) posuneme graf funkce. Na první pohled je vidět, že pro nulový bod odmocniny platí \(x=4\), tedy ve směru osy \(x\) posuneme graf o čtyři jednotky doprava. Po ose \(y\) posuneme graf o dvě jednotky nahoru. Graf funkce tedy bude mít počátek v bodě \([4;2]\). Zkuste početně určit definiční obor a váš výsledek porovnejte s grafem.
Příklad 10
Nyní se zaměříme na možnosti, jak lze modifikovat sudou odmocninu přidáváním záporného znaménka na různé pozice.
a) \(y=-\sqrt x\) b) \(y=\sqrt {-x}\) c) \(y=-\sqrt {-x}\)
Řešení 10
Všechny tři modifikace mají počátek v bodě \([0;0]\), každá však prochází jiným kvadrantem. Elementární funkce \(y=\sqrt x\) prochází I. kvadrantem, kterými však ostatní?
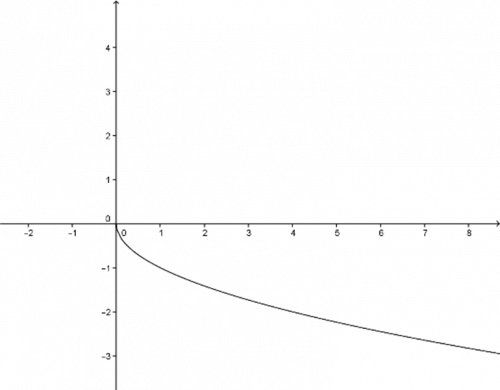
a) Předpis této funkce se od \(y=\sqrt x\) liší znaménkem před odmocninou. Záporné znaménko před odmocninou převrací graf funkce pod osu x. Zkuste si dosadit libovolná \(x\) z definičního oboru a uvidíte, že hodnoty závisle proměnné \(y\) opravdu vychází záporné. Graf funkce tedy prochází IV. kvadrantem.
b) Jak se změní definiční obor, pokud přidáme mínus k proměnné \(x\) pod odmocninu? Výraz pod druhou odmocninou musí být vždy větší nebo roven nule, řešíme tedy nerovnici \(-x\geq 0\). Vynásobením obou stran nerovnice číslem \(-1\) získáme podmínku \(x\leq 0\), tedy \(D(f)=(-\infty;0\rangle\). Tím se nám výběr správného kvadrantu omezil na dvě možnosti – na druhý a třetí. Nyní použijeme příklad a), ve kterém jsme si ukázali, že záporné znaménko před odmocninou převrací graf funkce pod osu x. V tomto příkladu však záporné znaménko před odmocninou není, tudíž graf zůstává nad osou x a leží ve druhém kvadrantu.
Poznámka: Pokud si nejsme jistí kvadrantem, stačí dosadit pár libovolných \(x\)z definičního oboru dané funkce a podle funkčních hodnot lehce rozhodneme, v jakém kvadrantu se pohybujeme. V příkladu b) můžeme z definičního oboru vybrat například \(x=-4\). Po dosazení do funkčního předpisu dostáváme \(y=\sqrt{-(-4)}=2\), tedy bod \([-4;2]\), který opravdu leží ve druhém kvadrantu.
Bod A je bod o souřadnicích \([-4;2]\).
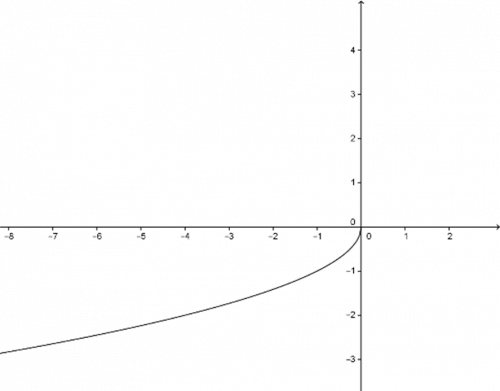
c) Poslední případ je kombinace dvou předchozích. Jaká \(x\) můžeme dosazovat do funkčního předpisu, aby dával smysl? Pouze nekladná, protože \(D(f)=(-\infty;0\rangle\). Jakých hodnot nabývá závisle proměnná \(y\)? Jelikož před odmocninou stojí znaménko mínus, nabývá hodnot záporných. Tudíž graf funkce leží v třetím kvadrantu. Pro ověření správnosti výsledku si znovu můžeme zvolit libovolné \(x\) z definičního oboru a dosadit do funkčního předpisu. Který kvadrant vychází?
Poznámka: Kvadranty kartézské soustavy souřadnic číslujeme od pravého horního kvadrantu proti směru hodinových ručiček.