V dnešním článku se podíváme na graf funkce třetí mocniny a její inverzní funkce, třetí odmocniny.
Kubická funkce je nejznámějším zástupcem funkcí s obecným předpisem \(y=x^{2k+1}, k\in N\) (\(2k+1\) je označení pro množinu lichých čísel). Funkce inverzní k funkci \(y=x^3\) je \(y=\sqrt[3] x\). Pro načrtání modifikovaných grafů kubické funkce platí pravidla, která již dobře známe, proto to vezmeme svižněji.
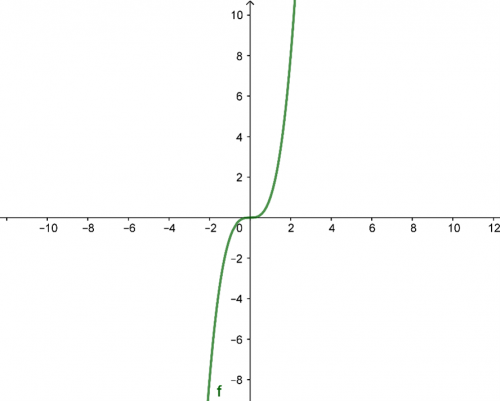
Funkce \(y=x^3\) má, stejně jako všechny polynomické funkce, definiční obor všechny reálná čísla, tedy \(D(f)=R\). Její graf vypadá následovně.
Čeho si oproti grafu kvadratické můžeme všimnout je, že graf funkce kubické má obor hodnot všechna reálná čísla, tedy sahá i pod osu \(x\). Proč? Protože pokud nějaké záporné číslo umocníme na třetí, dostaneme znovu záporné číslo. Např. pro funkci \(f(x)=x^3\), když \(x=-2\), dostaneme \(f(-2)=(-2)^3=(-2)*(-2)*(-2)=(-8)\).
Pojďme si nyní graf třetí mocniny modifikovat.
Příklad 1
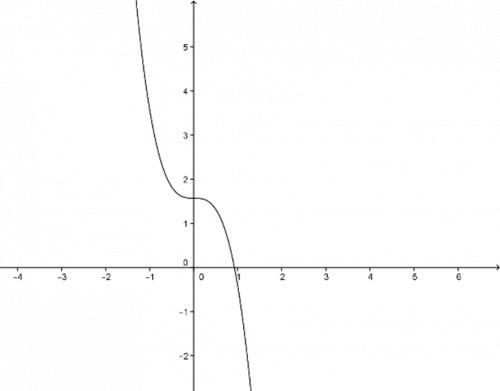
\(y=-2x^3+{\pi \over 2} \)
Řešení 1
Postup při načrtání grafů už známe. Záporné znaménko před \(x^3\) nám dává na vědomí, že graf je třeba překlopit. Dvojka před proměnnou \(x\) zapříčiňuje dvojnásobně rychlý růst hodnot závisle proměnné, tedy graf bychom správně měli načrtnout dvakrát hubenější. Jelikož nám však jde pouze o náčrt, nemusíme být tak přesní. Hodnota \({\pi \over x}\) udává posunutí ve směru kladné osy \(y\). Výsledný graf tedy vypadá takto.
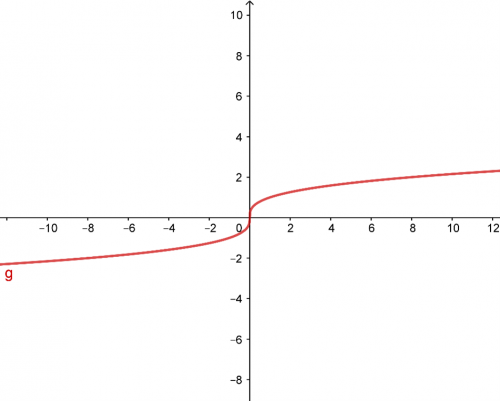
Třetí odmocnina je funkcí inverzní k třetí mocnině. Na rozdíl od druhé odmocniny má třetí odmocnina definiční obor všechny reálná čísla, tedy můžeme pod třetí odmocninu dosazovat i záporná \(x\). To vyplývá z toho, co jsme si popsali výše. Pokud platí, že \((-2)^3=-8\), tak třetí odmocnina čísla \(-8\) musí být znovu \(-2\), tzn. \(\sqrt[3] {-8}=-2\).
Základní graf třetí odmocniny vypadá následovně.
Pojďme si nyní tento graf modifikovat.
Příklad 2
\(y=\sqrt[3]{{x \over 4}-{\pi\over 2}}+7\)
Řešení 2
Podle nám již známých pravidel nejdříve určíme nulový bod odmocniny. Řešíme rovnici \({x \over 4}-{\pi\over 2}=0\), což nastane pokud \(x=2\pi\). Sedmička za odmocninou nám určuje co? Posunutí po ose \(y\) o sedm jednotek nahoru. Celý graf tedy posuneme o \(2\pi\) doprava po ose \(x\) a o 7 nahoru po ose \(y\).
Na obrázku jsou pro větší přehlednost zakresleny i osy \(x=2\pi\) a \(y=7\).