V předpisu lineární lomené funkce se proměnná x vyskytuje ve jmenovateli v první mocnině. Grafem lineární lomené funkce je hyperbola. Co se definičního oboru týče, je třeba ohlídat jediné – nulový bod jmenovatele.
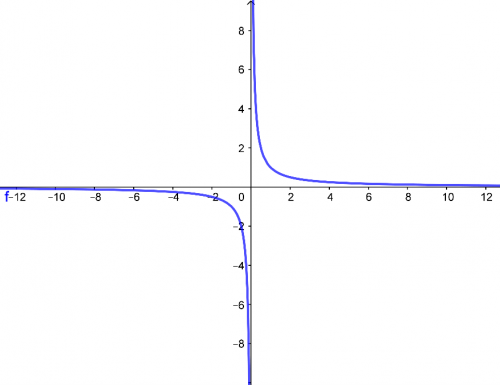
Základní graf lineární lomené funkce \(f(x)={1\over x}\) vypadá následovně.
Jak můžeme vidět na obrázku, graf nikdy neprotíná osu \(x\) ani osu \(y\). Definičním oborem jsou tedy všechna reálná čísla kromě nuly, \(D(f)=R/\{0\}\). Obor hodnot je na tom stejně, \(H(f)=R/\{0\}\). Jak se graf pozmění, pokud modifikujeme obecný předpis, si ukážeme na následujícím příkladu.
Příklad 1
\(y={5 \over {2x-3}}+2\)
Řešení 1
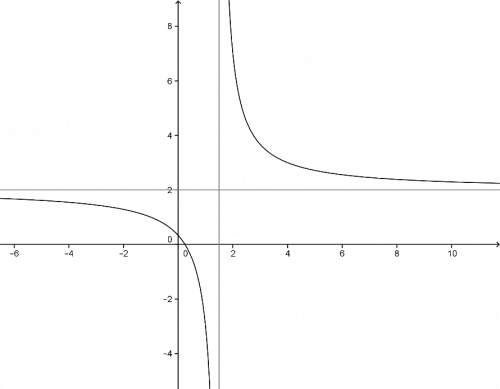
Při načrtání grafů lineárně lomených funkcí je výhodné do obrázku načrtnout i osy vzniklé posunutím grafu z počátku soustavy souřadnic. Vznikne tak pomocný kříž, podle kterého se lépe zorientujeme a ulehčíme si spoustu práce. Pomocný kříž je tvořen dvěma osami, ke kterým se graf funkce blíží, avšak nikdy je neprotne. Tyto osy se nazývají asymptoty. Jak zjistíme jejich rovnice? Nejprve nalezneme nulový bod jmenovatele. Řešíme tedy rovnici \(2x-3 = 0\), což nastane, pokud \(x={3\over 2}\). Následně posuneme graf funkce o dvě jednotky v kladném směru osy \(y\). První asymptota má rovnici \(x={3\over 2}\) a druhá \(y=2\). Načrtnutím asymptot do soustavy souřadnic získáme pomocný kříž, podél něhož se pnou ramena hyperboly.
Jak vidíme, ramena hyperboly se blíží k asymptotám, ale neprotínají je. Dalšími pomocnými body, které se vyplatí určit a zakreslit jsou průsečíky grafu funkce s osami kartézské soustavy (osa x a osa y). Jak se určí průsečíky, jsme si již ukázali, proto jen v rychlosti připomeneme. Hledáme-li průsečík s osou x, jeho ypsilonová souřadnice je vždy rovna nule. Hledáme-li průsečík s osou y, do předpisu funkce dosazujeme nulu za x.
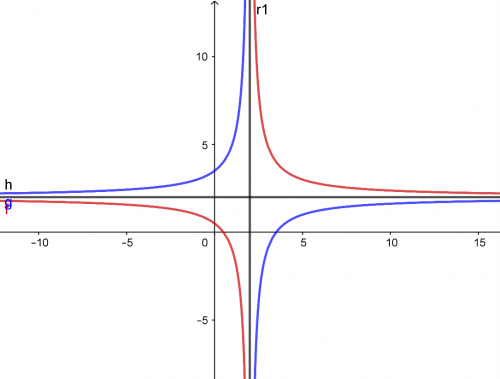
Pokud bychom před proměnou x měli v předpisu funkce záporné znaménko, graf se překlopí přes asymptoty do druhého a čtvrtého kvadrantu. Pro představu si ukážeme srovnání funkcí \(f(x)={3\over {x-2}}+2\) a \(g(x)={3\over {2-x}}+2 \).
Funkce \(f(x)\) je znázorněná oranžovou barvou a vidíme, že leží v prvním a třetím kvadrantu (nového kříže z asymptot). Naproti tomu funkce \(g(x)\), která je na obrázku modrá a má před proměnou x záporné znaménko, leží ve druhém a čtvrtém kvadrantu.
Lineární lomená funkce zadaná ve tvaru \(y={{ax+b}\over {cx+d}}\)
Příklad 2
\(y={{5x+2}\over {x-1}}\)
Lineární lomené funkce jsou velmi často zadány tak, aby rovnice asymptot nebyly na první pohled vidět. V takovém případě, stejně jako u kvadratických funkcí, je třeba předpis funkce nejdříve upravit. Pojďme si tedy ukázat, jak na to!
V první řadě se musíme naučit/připomenout si dělení mnohočlenu mnohočlenem. Jistě si všichni pamatujeme, když jsme se v první třídě učili dělení pod sebou. Dělení mnohočlenu mnohočlenem je obdobné.
1) Napíšeme si členy hezky vedle sebe, jako v první třídě, a první člen první závorky vydělíme prvním členem druhé závorky. V našem případě provedeme dělení \(5x\div x=5\).
\((5x+2) \div (x-1)=5\)
2) Následně vynásobíme náš dočasný výsledek s druhou závorkou a výsledek zapíšeme pod první závorku, od které jej odečteme. Pro náš případ roznásobíme následovně: \(5 \ast x=5x\) a \(5 \ast (-1)=-5\)
\((5x+2) \div (x-1)=5\)
\(-(5x-5)\)
Nezapomeneme před spodní závorku dát znaménko mínus!
3) V posledním kroku odečteme závorky pod sebou a zbytek připíšeme k výsledku prvního dělení. V našem případě po sečtení závorek pod sebou zůstalo sedm, což výrazem \((x-1)\) nelze dále beze zbytku dělit, proto zapíšeme k dosavadnímu výsledku ještě \(+{7\over {x-1}}\).
\((5x+2) \div (x-1)=5+{7\over {x-1}}\)
\(-(5x-5)\)
\(7\)
Předpis funkce \(y={{5x+2}\over {x-1}}\) se dá ekvivalentně zapsat také jako \(y=5+{7\over {x-1}}\). Z nového zápisu již dobře vidíme asymptoty \(y=5\) a \(x=1\), které vytvoří nový pomocný souřadnicový kříž.
Příklad 3
a) \(y={{3x+1}\over {x-2}}\) b) \(y={{-2x+2}\over {0.5x+3}}\) c) \(y={{4x+2}\over {2x+5}}\)
Řešení 3
a) Nejdříve si výraz přepíšeme vedle sebe a první člen první závorky vydělíme prvním členem druhé závorky, tedy
\((3x+1) \div (x-2)=3\)
Následně roznásobíme naším dosavadním výsledkem druhou závorku a výsledek zpětného násobení zapíšeme se znaménkem mínus pod první závorku.
\((3x+1) \div (x-2)=3\)
\(-(3x-6)\)
V posledním kroku závorky pod sebou sečteme a je hotovo.
\((3x+1) \div (x-2)=3+{7\over {x-2}}\)
\(-(3x-6)\)
\(7\)
Zůstalo nám sedm, což již výrazem \((x-2)\) nelze dále beze zbytku dělit, a tak zapíšeme \(7\over {x-2}\). Asymptoty grafu funkce mají rovnice \(y=3\) a \(x=2\).
b) Použijeme naprosto stejný postup. Jen si musíme dát pozor na záporné znaménko před proměnnou x ve jmenovateli.
\((-2x+2) \div (0.5x+3)=-4+{14\over {0.5x+3}}\)
\(-(-2x-12)\)
\(14\)
Vydělili jsme první členy závorek, roznásobili výsledkem prvního dělení jmenovatel (druhou závorku), odečetli výsledek zpětného násobení od první závorky a hotovo! Horizontální asymptota má rovnice \(y=-4\) a vertikální \(x=-6\) (získáme z rovnice \(0.5x+3=0\)).
c) \((4x+2) \div (2x+5)=2-{8\over {2x+5}}\)