Grafem lineární funkce je přímka. Lineární funkci poznáme tak, že proměnná \(x\) se vyskytuje vždy v první mocnině. Obecně se lineární funkce nechá zapsat vzorcem \(y=kx+q\), kde \(k\) je směrnice (s pojmem směrnice se ještě setkáme) a \(q\) je hodnota, o kterou budeme danou funkci posouvat po ose y. Uvedeme příklad a vše bude hned jasnější.
Příklad 5
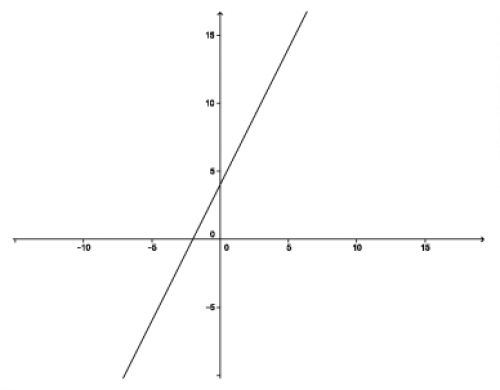
Na obrázku vidíme graf funkce \(y=2x+4\). Pokud porovnáme s obecným vzorcem lineární funkce, dostaneme \(k=2\) a \(q=4\). Z hodnoty směrnice \(k\) lze dopočítat, jaký úhel svírá graf funkce s osou x. Nám však zatím postačí fakt, že pokud \(k>1\), graf funkce je nakloněn blíže k ose y a pokud \(k<1\), graf je nakloněn blíže k ose x.
Hodnota q nám udává, o kolik jednotek bude graf funkce posunut po ose y. Pro nás \(q=4\), proto posuneme graf o 4 jednotky nahoru po ose y a tedy průsečík grafu funkce s osou y má souřadnice [0;4].
Poznámka: Průsečíky s osami se často dají velmi snadno dopočítat. Stačí si uvědomit, že průsečík s osou y bude mít určitě souřadnici x rovnou nule. Do předpisu funkce tedy za \(x\) dosadíme nulu a dopočítáme hodnotu \(y\). Náš případ řešíme následovně: \(y=2*0+4\) a tedy \(y=4\). Pro průsečík s osou x musí logicky platit \(y=0\). Řešíme \(0=2x+4\) a z toho plyne, že \(x=-2\). Průsečík grafu funkce s osou x má souřadnice [-2;0].
Příklad 6
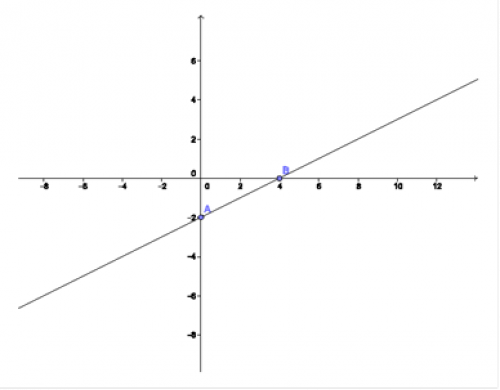
\(y={x \over 2}-2\)
Tento příklad si společně vyřešíme hezky od začátku. Jedná se určitě o lineární funkci, protože \(x\) se vyskytuje v první mocnině. Také platí \(k={1\over 2}\) a \(q=-2\). Grafem lineární funkce je přímka a jak víme již ze základní školy, přímka je určena dvěma body. Stačí nám tedy zvolit dva libovolné body, proložit jimi přímku a tím získáme graf lineární funkce. Zvolíme tedy libovolně například \(x=0\) a \(x=4\). Po dosazení \(x=0\) do předpisu funkce dostáváme \(y=-2\) a po dosazení \(x=4\) dostáváme \(y=0\). Získali jsme tedy body \([0;-2]\)a \([4;0]\). Proložením přímky těmito body získáme hledaný graf, který je opravdu nakloněn blíže k ose x a posunut o dvě jednotky dolů po ose y (což jsme zjistili již z hodnot \(k\) a \(q\)).
Shrnutí
Pokud chceme načrtnout graf lineární funkce, stačí nám dopočítat dva libovolné body a proložit jimi přímku. Hodnoty \(k\) a \(q\) slouží jen pro ověření.